חומר עזר 8.1 : האינטגרל המסויים והלא-מסויים

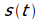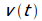בפרק 5.1, הצגנו באופן אינטואיטיבי את הפעולות של גזירה ואינטגרציה כפעולות הפוכות הקושרות בין פונקציית המרחק-עד-כהובין המהירות . מכך חילצנו את המשמעות הגיאומטרית של הנגזרת כשיפוע של המשיק (5.4) ושל האינטגרציה כשטח-עד-כה (5.6). למעשה, כשהרעיון של שיפוע המשיק מובע באופן ריגורוזי, אם על ידי הסתכלות על שיפוע המיתר המגביל, או על ידי הסתכלות על השיפוע של הקירוב הלינארי (משיק), מגיעים להגדרה הריגורוזית של הנגזרת (5.4).

כאשר מביעים את הרעיון של שטח מתחת לגרף באופן ריגורוזי, על ידי שימוש במלבנים לקירוב השטחים של רצועות "רזות" מתחת לגרף, וחלוקה של השטח לרצועות דקות יותר ויותר, מגיעים להגדרה הריגורוזית של האינטגרל המסויים

דרך סכומי רימן (ראה 5.6).

מצד שני, מחשבה על הפעולה של אינטגרציה כפעולה ההפוכה לנגזרת נותנת את ההגדרה של אינטגרלים לא מסויימים בה נעשה שימוש במהלך פרק 7:

הקשר בין שני המושגים הללו:

ניתן על ידי המשפט היסודי של החשבון האינפיניטסימלי, לפיו תחת תנאים מסויימים על הפונקציה

פונקציית השטח-עד-כה היא פונקציה קדומה.