חומר עזר 6.9 : טורי טיילור ודוגמאות ידועות

שימו לב שפולינום טיילור:

משתנה כשr גדל ל-r+1, רק בהוספה של עוד איבר אחד. ואכן, הוא סכום חלקי של הטור:

ובו (בפולינום שהוא הסכום החלקי) (r+1) האיברים הראשונים מתוך הטור. אם התשובה לשאלה 1(B6.8) היא חיובית, אנחנו אומרים שהטור (*) מתכנס ב.

אם התשובה לשאלה 2 (B6.8) היא חיובית, אנחנו אומרים שהטור (*) מתכנס ב ל.

הטור (*) נקרא טור טיילור שלf סביב ומשמעותו באה לידי ביטוי בסכומים החלקיים שלו הם הם פולינומי טיילור .

במקרים בהם התשובה לשאלה 2 (B6.8) היא חיובית, אנחנו כותבים ש:

הוא ערך הטור, כלומר המספר אליו הסכומים החלקיים של הטור, , מתכנסים כאשרr גדל.

שאלה 3 עוסקת בקצב ההתכנסות של הטור, ובה נתעמק ב-6.11 ו-6.12.

כאן נרשום את התשובות (החיוביות) לשאלות 1, 2 עבור כמה פונקציות ספציפיות, כולן בפיתוח הטור סביב הנקודה x=0 (כלומר, a=0). שימו לב שקביעת טור טיילור (*) עבור פונקציה מסוימת מתמצה במציאת נגזרות מסדרים גבוהים יותר בנקודה a (כמו ב6.7) אבל שאלת ההתכנסות עצמה דורשת אנליזה שנמצאת מעבר לחומר של קורס זה.

תוצאות:

בעמודה הראשונה מצויינת הפונקציה. בעמודה השנייה מופיע טור הטיילור שלה (חושב כמו ב6.7). אף בעמודה השלישית מופיע טור הטיילור, עתה מנוסח כסכום עם נוסחה עבור האיבר הכללי. משמעות סימן השוויון בין העמודה הראשונה והשנייה היא שטור טיילור מתכנס לפונקציה(התשובות לשתי השאלות ב6.8 הן חיוביות), אבל רק עבור ערכים ספציפיים של x השייכים לתחום המפורט בעמודה האחרונה (מה שנקרא תחום ההתכנסות).

החישובים של טורי טיילור [בשורות הטבלה] 1, 2 ,4 מפורטים ב6.7. 3 הוא בדיוק כמו 2; 5 הוא אפילו יותר פשוט מ-4. 7 הוא בדיוק כמו 5, בעוד ש-6 הוא קשה מאוד בחישוב ישיר, והרבה יותר קל אם משתמשים בטריקים המופיעים ב- 6.10. 5 הוא המקרה היחידי בו נוכל לבצע אנליזה מלאה באמצעות הכלים שעומדים לרשותנו: ראה משאב הדוגמאות 6.9 (C6.9).

טור הבינום

7: עבור, גוזרים שוב ושוב:

כך ש. כך מתקבל טור הטיילור המופיע בטבלה (בטבלה הפיתוח הוא סביב x=0).

זו היא דוגמה חשובה, ששמה הטור הבינומי:

בשל הדמיון בין הנוסחה הזו ובין הנוסחה של המקדם הבינומי כאשר :

המקדמים בטור הבינומי נקראים גם מקדמים בינומיים ומוגדרים ע"י הנוסחה:

(כמובן שאי אפשר להשתמש עכשיו בהגדרה., מאחר והעצרת של ערך לא שלם אינה מוגדרת[אלא אם כן משתמשים בפונקצית גאמה- ראה פרק 8]).

בסימון זה, הטור הבינומי הוא:

ההסבר לתחום ההתכנסות של הטור הבינומי- הוא לא טריוויאלי ונמצא מעבר לחומר של קורס זה.

שימו לב: כאשר היא מספר שלם לא שלילי,

וכך בטור הבינומי רק (n+1) האיברים הראשונים לא מתאפסים, ואכן זו פשוט נוסחת הבינום:

והוא "מתכנס" עבור כל x (זהו אך סכום סופי-פולינומי טיילור הם סכומים חלקיים עבור r<n ומשתווים לפולינום עצמו עבור, כמו בסעיף 6.7 , 1 [בגירסה האנגלית B6.7A]).

דוגמה:

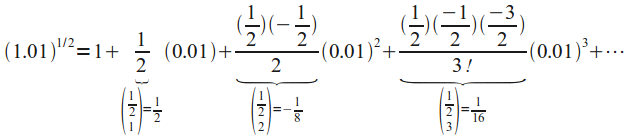
האיברים מתחלפים בסימן וקטנים מהר מאוד, ולכן

עובדה כללית (שנוכל להוכיח רק במת"פ 2) היא שתחום ההתכנסות של טור חזקות (ומכאן של כל טור טיילור) במספרים הממשיים הוא קטע סימטרי סביב נקודת הפיתוח (a, במקרה שלנו), אם כי הוא יכול להיות סגור או פתוח (באופן בלתי תלוי) בשני קצותיו [קרי- כל האפשרויות יתכנו- סגור באחד פתוח בשני וכו'].

אז לטור טיילור של הפונקציה סביב הנקודה x=a יהיה תחום התכנסות מהצורה הבאה: