חומר עזר5.6 : הגדרת האינטגרל המסוים


כדי למצוא את השטח תחת הגרף של f בין ל- , מקרבים את הפונקציה ע"י פונקציית מדרגה. בוחרים חלוקה של הקטע בעזרת הנקודות:



ואז השטח תחת הגרף מקורב ע"י:





שהוא סכום שטחי המלבנים שגובהם ורוחבם . כלומר השטח תחת הגרף של פונקציית המדרגה שערכה קבוע בקטע . (ראה 5.3 לפירוט האינטואיציה הפיזיקלית העומדת מאחורי סכום כזה). סכום זה נקרא סכום רימן (Riemann sum).


אם הסכום מתקרב לערך מסוים כשהחלוקה נהיית עדינה יותר ויותר (כלומר כש- n גדל והרוחב המקסימלי ) נאמר ש- f אינטגרבילית בקטע , והערך אליו מתקרבים נקרא ערך האינטגרל של f על והוא מסומן או .



הערות:

1

כל הפונקציות הרציפות הן אינטגרביליות לפי הגדרה זו.


2

כל הפונקציות הרציפות למקוטעין הן אינטגרביליות (הכוונה היא לפונקציות המוגדרות ע"י הגדרות נפרדות על תת-קטעים המושרים ע"י חלוקה כלשהי של , באופן בו הפונקציה רציפה בכל תת-קטע של החלוקה, ונקודות אי רציפות (“קפיצות”) עשויות להופיע בנקודות החלוקה בלבד).


3

    אין סיבה מיוחדת לבחור לדגום את f בכל תת-קטע דווקא מקצה תת הקטע השמאלי , ניתן להשתמש ב:


    או באופן כללי יותר


    כש- נמצאות ב- . כל אלה נקראים סכומי רימן גם כן. ניתן גם להשתמש בסכומים:


,


    שנקראים סכומי דרבו (Darboux sums) – הם נותנים חסמים מלעיל ומלרע לשטח. משתמשים בהם בתאוריה של אינטגרציית רימן, אבל הם לא כ"כ שימושיים לחישובים, שכן צריך לדעת את ערכי המינימום והמקסימום של f ב- , ואלא אם כן הם במקרה בנקודות הקצה, זה עשוי להיות מסובך.



4*

    לא כל הפונקציות הן אינטגרביליות לפי ההגדרה שלנו.

    למשל: לא אינטגרבילית על . (סכומי רימן על חלוקות עדינות יכולים לקבל כל ערך בין 0 ל- 1.)



5

    הגדרה זו של אינטגרביליות ידועה כאינטגרביליות רימן. בפועל, כל הפונקציות שניתקל בהן במהלך הקורס תהיינה אינטגרביליות (למעט שאלות של התכנסות כשנעסוק באינטגרלים לא אמיתיים (/ מוכללים) (Improper integrals). יש מושג כללי יותר של אינטגרביליות, אינטגרביליות לבג (Lebesgue integrability), שתחתיו כל הפונקציות שהן אינטגרביליות רימן הן עדיין אינטגרביליות, אבל אליהן מתווספות מספר פונקציות נוספות, שהן אינטגרביליות לפי הגדרת לבג אבל לא אינטגרביליות לפי הגדרת רימן (כמו הפונקציה בסעיף 4). אלה מחוץ לתחום קורס זה.



6

    בפרק זה נדון בהגדרה הפורמלית של אינטגרל רימן, וניתן דוגמה להגדרה זו (מתחת) עבור פונקציה פשוטה. חישוב מעשי של אינטגרלים מושג בדרך שונה (אם זה אפשרי אנליטית) – ראה פרקים 7,8.



7

    כדי לחשב נומרית את ערכם של אינטגרלים משתמשים בשיטה הדומה לסכום רימן, רק שבהינתן מספר בדיד של ערכי הפונקציה, ניתן לקבל הערכה טובה יותר של השטח ע"י קירוב לפונקציה שאינה פונקציית מדרגה (קבועה למקוטעין). קירוב לינארי למקוטעין נותן את החוק הטרפזי (Trapezoidal rule), קירוב ריבועי למקוטעין נותן את חוק סימפסון (Simpson's rule), ובאופן כללי ניתן לקרב למקוטעין ע"י פולינומים מדרגה גבוהה יותר.



8

    ניתן להגביל את הדיון לסכומי רימן בהם החלוקות הן של n תתי-קטעים שווי גודל: ואז סכום רימן הוא פשוט:





דוגמה: ניקח את הפונקציה בקטע [0,1]. אם נשתמש רק בדגימה אחת של v ב- נקבל הערכה לא טובה של המרחק שנחצה בקטע [0,1]:

שמתאים לחלוקה [0,1] עם :



אם נחלק את [0,1] לשני תתי-קטעים שווים, :





אם נחלק את [0,1] ל 10 תתי-קטעים שווים (n=10), נקבל הערכה טובה עוד יותר לשטח:




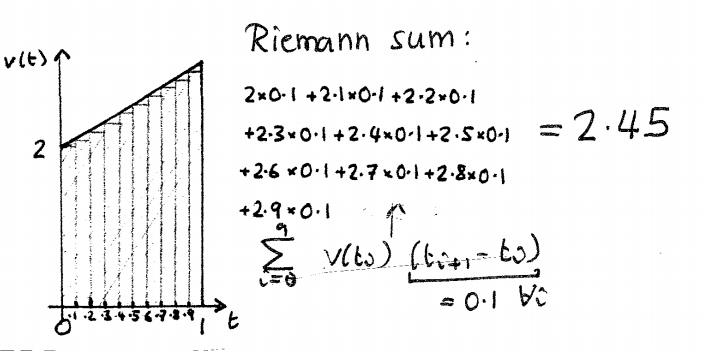
נראה שהמספרים מתקרבים ל- 2.5 כש- n גדל, אז . כדי לבדוק זאת אלגברית, נמצא נוסחה לסכום כשמחלקים ל- n חלקים שווים. אז



ולכן סכום רימן הוא:




או בכתיב ארוך:

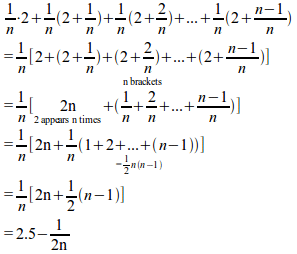
שאכן מתקרב ל- 2.5 עבור n גדול. בד"כ, לפונקציות יותר מסובכות, לא נוכל למצוא נוסחה סגורה לסכום רימן, לכן נאלץ להשתמש בטכניקות אחרות כדי לחשב את האינטגרל (ראה פרקים 7,8).


הערה לגבי סימון: כפי שהוזכר ניתן לכתוב את האינטגרל המסוים של f בקטע [a,b] כ-


או



לרוב הפונקציות אין "שמות" יפים (כמו sin או exp), וצריך לבטא אותן ע"י הנוסחה שלהן. כדי לתת נוסחה צריך משתנה, וברגע שמציינים משתנה יש להוסיף גם "dt”. מדוע "dt”? האם יש קשר ל- “dt” של הנגזרת? התשובה היא כן:


“dt” - שינוי קטן ב- t




לכן קירוב סכום רימן



הופך ל- ()

כמו ש- הפך ל- .


המשתנה t נקרא משתנה דמה – ניתן להחליף אותו בכל אות אחרת שלא נעשה בה שימוש, אך יש להחליף את האות גם ב- “” וגם ב- “dt” במקביל:





שטחים שליליים

מהגדרת סכומי רימן ניתן לראות שערך שלילי של f תורם תרומה שלילית לסכום רימן



וכך תורם תרומה שלילית לאינטגרל (שטחים מתחת לציר ה- x תורמים תרומה שלילית לאינטגרל).


יש עוד מקרה בו שטחים נמנים כשליליים – אלה שנספרים "אחורה", עם . יש שני הסברים לסיבה ש-

  1. במקרה של פונקציה v שהיא המהירות של גוף שנע במימד אחד בזמן t, מייצג את מיקום הגוף בזמן t, הנמדד ביחס למיקומו בזמן 0. אם , אז הגוף נע בכיוון החיובי, לכן






כלומר, בזמן שלילי, כדי להשתמש בביטוי חייבים להגדיר:




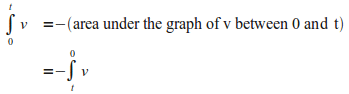
  1. נרצה שתמיד יתקיים .

    משוויון זה נסיק:

    ואם נרצה שיתקיים ,

    נאלץ להגדיר: .