חומר עזר 5.17 : משפט הערך הממוצע

משפט הערך הממוצע: תהי פונקציה רציפה, גזירה בכל נקודה בקטע הפתוח . אזי קיימת נקודה כך שמתקיים:

גאומטרית, משמעות הדבר היא שקיימת נקודה בפנים הקטע, כך שהמשיק לגרף של f בנקודה זו מקביל למיתר המחבר את תמונות נקודות הקצה x=a , x=b.

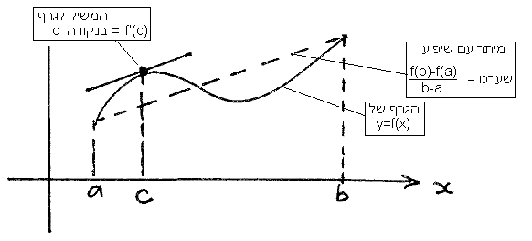
ייתכן שתהיה יותר מנקודה c אחת כזו, אך המשפט מבטיח את קיומה של לפחות נקודה c אחת המקיימת את השוויון.

המשמעות האינטואיטיבית: נניח כי אנו מיישמים את משפט הערך הממוצע על הפונקציה, שמייצגת מיקום של מכונית בזמן t , על כביש נתון. אם t=a, t=b הן נקודות הזמן שבהן המכונית נכנסת ויוצאת מהכביש בהתאמה (לעיתים אלה נחתמות על כרטיס), אזי הערך

יכול להיות מחושב בקלות. משמעותו היא המהירות הממוצעת של המכונית בכביש (ובנוסף לכך, במקרה זה, מכיוון שמדובר בבעייה חד-מימדית זה גם ה-speed- הגודל הנמדד ע"י המכונית בעת נסיעתה).

אם ערך זה הנו מעבר למגבלת המהירות בכביש הנתון, אזי משפט הערך הממוצע מצביע על כך שקיימת נקודת זמן פנימית c שבה המהירות הרגעית הייתה שווה לערך המהירות הממוצע שהתקבל – כך שאפילו ללא מצלמת מהירות, יש לנו הוכחה שהמכונית נסעה במהירות שהיא מעבר למהירות המותרת!

זוהי גם הסיבה לשם המשפט “הערך הממוצע” - זה מראה שהמהירות הממוצעת בקטע תמיד מתקבלת באופן רגעי באיזו שהיא נקודה פנימית בקטע.

לדוגמא: חותמות הזמן 09:21 , 10:15 (קטע זמן של 54 דקות) בקטע כביש באורך 91 ק"מ, מצביעות על ממוצע של

שהתקבל בנקודה כלשהי בקטע הזמן שלנו.