-
(סכום)
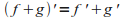
(מכפלה)
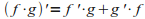
(מנה)

(הרכבה)
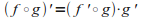
(כלל השרשרת)
(פונקציה הפוכה)
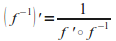
חומר עזר 5.12 : סיכום של חוקי גזירה וטבלת נגזרות של פונקציות אלמנטריות
בסעיף זה אנו מרכזים את כללי הגזירה מתתי הפרקים B 5.9, B 5.10, B 5.11 עבור פונקציה שרירותית הנתונה באופן סגור (פונקציה הנתונה כהרכבה של סכומים, מכפלות ופונקציות בסיסיות). מספר דוגמאות נוספות (וחשובות) מצורפות כאן, שאותן לא פיתחנו באופן מפורש בתתי הפרקים הקודמים ; ההסברים לדוגמאות אלו ניתן בסוף תת-פרק זה. בהמשך, סעיף 5.13 מדגים את השימוש בכלים אלו לצורך גזירת פונקציות שונות (הנתונות בצורה סגורה).
חוקי גזירה:
|
(סכום) |
|
|
|
(מכפלה) |
|
|
|
(מנה) |
|
|
|
(הרכבה) |
|
(כלל השרשרת) |
|
(פונקציה הפוכה) |
|
|
(באופן כללי איננו משתמשים בחוק האחרון, משום שהפונקציות ההפוכות לפונקציות האלמנטריות ונגזרותיהן מופיעות בטבלה המופיעה מתחת)
טבלת נגזרות של פונקציות אלמנטריות:

הערות :
בסעיף
5.10
פיתחנו
את הנגזרת של
![]() ושל
ושל
![]() .
שניהם
מקרים מיוחדים של
.
שניהם
מקרים מיוחדים של
![]() .
.
כיצד
ניתן להתמודד עם המקרה הכללי?
התשובה
– על ידי
שימוש בהגדרה
![]() :
:
|
|
|
כדרוש.
2. הפונקציות ההיפרבוליות כולן מוגדרות על ידי נוסחאות הדומות לנוסחאות הפונקציות
הטריגונומטריות, תחת החלפת sin, cos ב cosh, sinh.
מאחר ומתקיים:
|
|
|
אנו
יכולים לגזור פונקציות אלו בקלות,
ביודענו
כעת כי
![]() :
:
![]()
![]()
בדיוק כפי שפיתחנו את הנגזרות של tan, cot, sec , csc מהנגזרות של sin , cos בסעיף B 5.10, כך אנו יכולים לקבל את הנגזרות של tanh, coth, sech, csch מאלו של sinh , cosh (יש לשים לב לשינוי הסימן). באופן דומה זה יתבצע עבור הפונקציות ההפוכות כמופיע בסעיף B 5.11.
דוגמה:
למציאת
![]() :
:
נציב
![]() =y
ואז
מתקיים:
=y
ואז
מתקיים:
![]() =x
,
=x
,
![]() ,
ונקבל:
,
ונקבל:
|
|
|
אבל
![]() דהיינו
דהיינו
![]() וכן
וכן
![]()
![]()
(![]() =y
הוא
תמיד אי-שלילי
לפי מוסכמה,
כך
ש-
=y
הוא
תמיד אי-שלילי
לפי מוסכמה,
כך
ש-![]() הוא
השורש החיובי מבין הפתרונות)
הוא
השורש החיובי מבין הפתרונות)
ואז
![]() דהיינו
דהיינו
![]()