חומר עזר 4.3 : פונקציות הפוכות

אם הגרף של f חותך כל ישר המקביל לציר X (ישר מהצורה y=const) פעם אחת לכל היותר, נאמר ש-f היא חד-חד ערכית (חח"ע). המשמעות של היות חח"ע היא ש:

כלומר, כל ערך מושג (הפונק' משתווה אליו) פעם אחת לכל היותר.

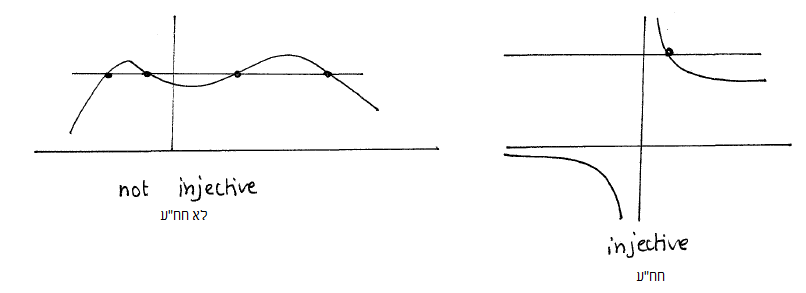
במקרה זה ניתן גם לומר ש-f היא הפיכה (על D).

הערה: לעתים קרובות התאמה (פונקציה) בין קבוצות נקראת הפיכה כאשר היא גם חח"ע וגם על. בהגדרה שנכתבה לעיל ובה אנו נשתמש ויתרנו על התנאי ש-f תהא על (דהיינו, התנאי שכל הערכים ב-B מושגים) ונעדיף לומר ש-f הפיכה (על תחום ההגדרה שלה D) אם f היא חח”ע. במקרה זה, ההתאמה

היא גם חח"ע וגם על (על, מכיוון שבחרנו את הטווח להיות בדיוק התמונה של התחום) בכל מקרה. משמעות הדבר היא שנתעלם מאפשרות הבחירה של הטווח כאשר נדון בהפיכותה של פונקציה.

לפונקציה f שהיא הפיכה על D קיימת פונקציה הפוכה:

אשר תחום ההגדרה שלה היא תמונת f .

לעתים קרובות פונקציה תהא לא הפיכה, אבל הפונקציה הנוצרת מהגבלת לתחום קטן יותר D, כן תהווה פונקציה הפיכה.

דוגמאות:

גרף של פונקציה הפוכה

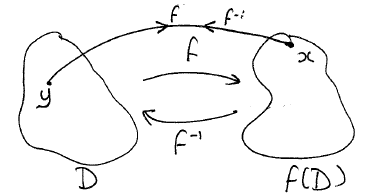
נניח ש-f היא פונקציה הפיכה. אז הפונקציה ההפוכה מוגדרת על ידי הכלל:

מוגדרת ע"י הכלל:

כלומר, שולחת את x לערך ש-f שולחת בחזרה ל-x.

הגרף של מורכב מהנקודות שעבורן קיים:

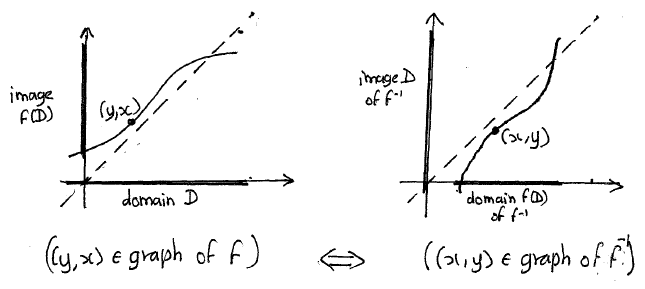
כלומר הגרף של הוא תמונת המראה של הגרף של f סביב הישר .

הערה: אין קשר בין הפונקציה ההפוכה לבין פונקצית המנה :