חומר עזר 4.2 : תחום הגדרה ותמונה

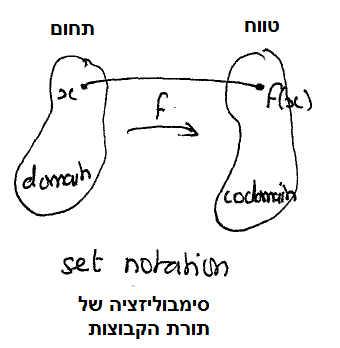
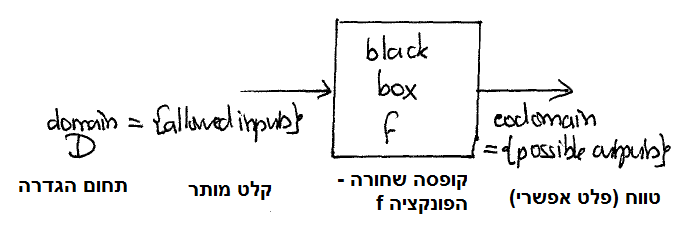
התחום (או תחום ההגדרה) של פונקציה הוא קבוצת הקלט המותר (החוקי) שלה. התמונה (או טווח) של פונקציה היא קבוצת הפלט האפשרי שלה.

את התמונה ניתן לסמן על ידי:

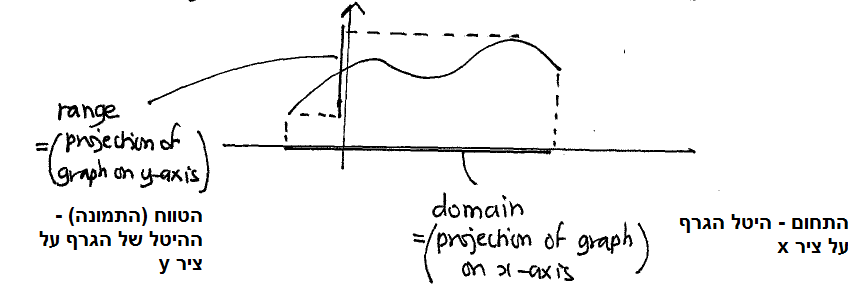
בגרף של פונקציה f ניתן לזהות את התחום ואת התמונה:

דוגמאות:

צמצום של פונקציה

אם היא פונקציה ו-A היא תת קבוצה של D, אז במינוח "הצמצום של f ל-A", אנו מתכוונים לפונקציה

(“f מצומצמת ל-A”) המוגדרת בדיוק לפי כלל ההתאמה של f, רק עם תחום קטן יותר, A. הטווח של פונקציה זו יהיה תת קבוצה של הטווח של f:

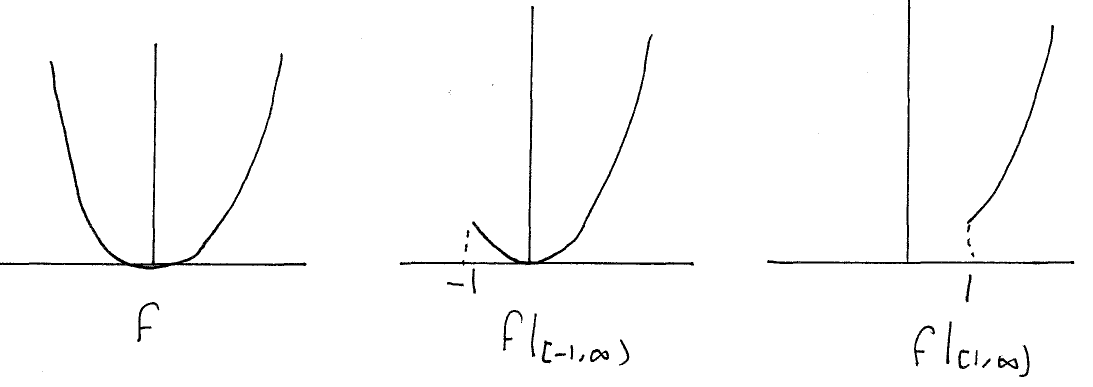
דוגמה:

צמצום ל ייתן שתי פונקציות שונות:

הגרף של הצמצום של f לקבוצה A הוא תת קבוצה של הגרף של f: