חומר עזר 4.17 : גרפים של הרכבות

בהנחה שאנו יודעים את הגרף של פונקציה g, אנחנו רוצים להבין איכותית את גרף ההרכבה של במקרה ש f היא פונקציה פשוטה, בדרך-כלל מונוטונית או "כמעט" מונוטונית. מספר דוגמאות ידגימו את העיקרון.

א.

זו היא ההרכבה של עם פונקציית הערך המוחלט. למרות שפונקציית הערך המוחלט אינה מונוטונית, קל להבין את ההבדל בין הגרפים של ו - הם זהים כאשר ונבדלים בשיקוף ביחס לציר ה-x בקטעים בהם .

ב. הרכבה עם

אנחנו כבר מבינים את ההשפעה של הרכבות עם פונקציות פשוטות אלה. אם , אז:

אם :

ג.

הפונקציה היא הרכבה של sin ו ln, אז נתחיל עם הגרף של sin. הפונקציה ln היא מונוטונית, מוגדרת רק על הממשיים החיוביים. אז תהיה מוגדרת רק היכן ש , כלומר על

מכיוון ש ln היא מונוטונית עולה, f תעלה היכן שsin x עולה, ותרד היכן שsin x יורדת. מכיוון שsin x היא מחזורית, מחזור , כך גם כל פונקציה שלה, אז נתעסק במרווח (אינטרבל) אחד, נאמר :

אז נקבל את הגרף:

ד.

זו היא הרכבה של הפולינום עם הפונקציה (פונקציה מונוטונית על מספרים ממשיים חיוביים [בנפרד] או שליליים [בנפרד]).

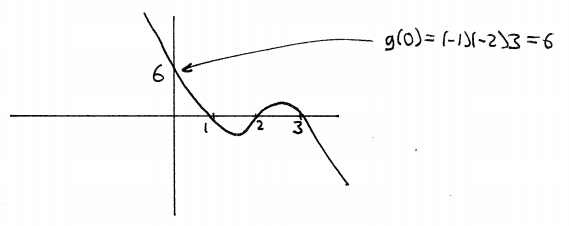
אז תחילה נשרטט את הגרף של . זהו פולינום עם שורשיםוממעלה 3 כאשר המקדם המוביל (המקדם של ) הוא 1-.

מעלה 3 (): x חיובי וגדול => גדול ושלילי.

x שלילי וגדול =>גדול וחיובי.

הפונקציה מוגדרת כאשר כלומר .

כעת נעבור על ערכי x, מהערכים השליליים הגדולים עד לחיוביים הגדולים, ונחקור את השינויים החשובים אשר משפיעים על . חשוב לשים לב היכן יורדת / עולה והיכן היא מחליפה סימן.

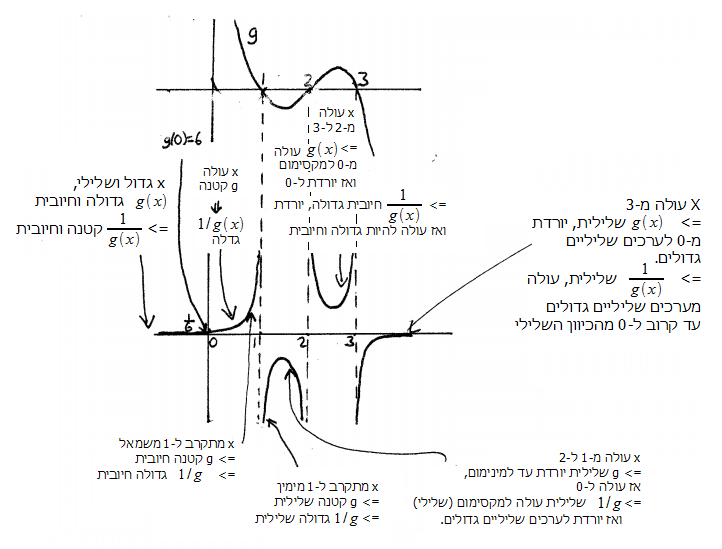
על מנת להבין את מבנה הגרף של f, מספיק לזהות : היכן האסימפטוטות (וy=0 ), הסימן של f והיכן היא עולה ויורדת. המיקום המדויק של המקסימום והמינימום המקומיים של f הינו זהה עבור g, אך קשה למצוא אותם ללא חדו"א (פרק 5). אך את הצורה האיכותית של f הצלחנו לפענח אף ללא חדו"א.

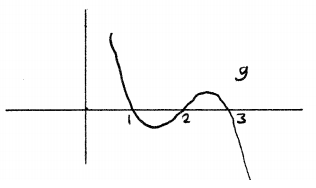
ה.

הפונקציה הזו היא הרכבה של הפולינום מסעיף ד יחד עם פונקצית ה- (פונקציה מונוטונית).

אז f מוגדרת היטב כאשר כלומר .

שוב אנו סורקים לאורך הקטעים בתחום ההגדרה של f:

כדי לראות איזו מהאפשרויות האלו מתארת את הצורה האיכותית של הגרף של f, שים לב:

ובצורה דומה ליד 2 ו-3.