חומר עזר 3.4 : הגדרת מספר מרוכב ומישור מרוכב

כאשר אנו מדברים על מספר מרוכב אנו מתכוונים לסימול הפורמלי

בו הם מספרים ממשיים. מספרים מרוכבים מסומנים על-ידי אותיות יחידות כגון ו-. עד שלב זה טרם ניתנה משמעות לחלק "" באמצע הביטוי - מספר מרוכב, לפי הגדרה זו, הוא רק זוג סדור של מספרים ממשיים, כמו וקטור ב-.

הערה: לעתים הסימן '' משמש במקום '' או אפילו . (בחשמל, או משמש לביטוי זרם, ולכן ישנו צורך בסימול שונה עבור ).

עבור מספר מרוכב, ,

הוא החלק הממשי של , המסומן או .

הוא החלק המדומה של , המסומן או .

הערה: משמש גם לייצוג התמונה של פונקציה (image) וגם לייצוג החלק המדומה (imaginary) של מספר ממשי. ניתן להבדיל בין השניים בדרך כלל לפי ההקשר.

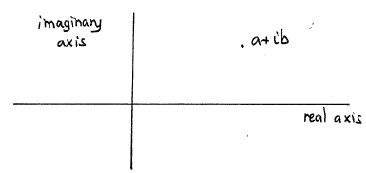
ק

ניתן לייצג מספרים מרוכבים באמצעות נקודה במישור בעלת קואורדינטות . בייצוג זה (הידוע בכינוי דיאגרמת Argand או המישור המרוכב), הצירים נקראים הציר הממשי והציר המדומה, וכל נקודה במישור מייצגת מספר מרוכב.

נקודה על הציר הממשי מייצגת מספר מהצורה (זאת אומרת, מספר ממשי בלבד).

נקודה על הציר המדומה מייצגת מספר מהצורה (זאת אומרת, מספר מדומה טהור).

הדבר מקביל לייצוג של מספרים ממשיים על הציר הממשי.