חומר עזר 3.2 : מבוא למספרים מרוכבים – משוואות ממעלה שלישית

בהנתן משוואה כללית ממעלה שלישית, אחרי חלוקה (אם צריך) במקדם של תמיד נוכל לדעת שהמשוואה המתקבלת הינה כזאת שהמקדם המוביל שלה הוא 1 (monic polynomial):

כמו שהשלמנו לריבוע לפולינום ממעלה שניה, נוכל כאן להשלים "לקוביה" ע"י הצבה ואז נקבל משוואה של ממעלה שלישית בה מקדמו של מתאפס:

(כאן הן ביטויים של ).

לכן בשביל לפתור כל משוואה ממעלה שלישית כללית, די אם נוכל לפתור משוואות ממעלה שלישית בהן מקדם האיבר הוא אפס.

קיימת השיטה של del Ferro (בסביבות 1526) ושל Tartaglia (בסביבות 1535) שפורסמה ע"י Cardano (בסביבות 1543) בה הפתרונות ל מבוטאים באופן הבא:

כבמשוואות ריבועיות, מופיע ביטוי תחת שורש ריבועי:

הידוע כדיסקרימיננטה (discriminant).

שורשים של משוואות ממעלה שלישית (cube roots) קיימים לכל מספר (ממשי), חיובי או שלילי. לכן המעכב היחידי בשימוש ב-(#) הוא כאשר . כאשר , מתקבל בעזרת (#) פיתרון ממשי יחיד.

גיאומטריה

כעת נביט בפן הגיאומטרי של הבעיה.

פתרון למשוואה

נתון ע"י החיתוך של הגרף עם ציר ה-. אך גרף של משוואה מדרגה שלישית נראה כך:

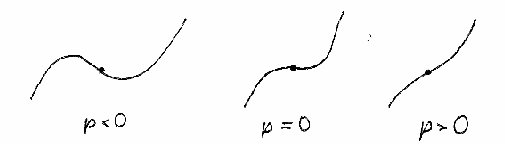
(בכל מקרה, הנקודה המסומנת, נקודת הפיתול (inflection point), נמצאת ב-, אבל המיקום היחסי של ציר ה-תלוי ב-)

כתלות ב-, ישנן אפשרויות רבות:

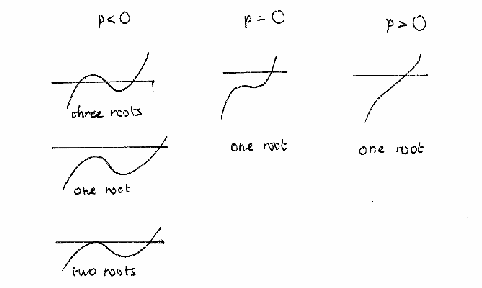
אפשר לראות שתמיד יש לפחות שורש אחד ממשי, אך יכולים להיות עד שלושה שורשים ממשיים.

פירוק לגורמים (Factorization)

כתמיד, לכל פולינום, הוא שורש אם"ם הוא גורם. לכן שלושה שורשים ממשיים, , מאפשרים פירוק לגורמים ממעלה ראשונה:

במקרה בו שני שורשים ממשיים עם נקודת השקה ב-נקבל:

עתה שוב חילקנו את הפולינום לגורמים (ממשיים) לינאריים.

בכל המקרים עם שורש ממשי אחד (חוץ מכאשר – אז שלושת השורשים הם )

לקבועים כלשהם, ובידיעה שלמשוואה אין שורש ממשי (הרי אחרת, הם יהוו שורשים ממשיים נוספים ל-) נסיק שאי אפשר לפשט את הפונקציה יותר מעל הממשיים. ז"א שאי אפשר לפרק אותה לגורמים ממשיים לינאריים.

אפשר להראות (בעזרת פרק 5) שהתנאי לקבלת שלושה שורשים ממשיים הוא ש-ו-. המקרה של השורש המרובה מתאים ל- ו-. לכן בדיוק במקרה בו (כשיש שלושה שורשים ממשיים) משוואת Cardano (#) לא מצליחה לתת לנו כל פתרון ממשי ע"י פירוש ישיר שלה!

שימו לב: , כך שרק כאשר , יכול להיות שלילי.

המקרה בו נפתר באופן מלא ע"י (#), שנותן פתרון ממשי אחד, אבל עבור המקרה בו לא ניתן לקבל מ- (#) אף פתרון אם עובדים רק עם מספרים ממשיים. בסביבות 1550, Bombelli הציע שיטה בה משתמשים באופן פורמלי בשורשים של מספרים שליליים ממנה ניתן להבין כיצד (#) מניבה שלוש תוצאות ממשיות. לצורך כך יש להשתמש ב"מספרים המדומים" הללו באופן פורמלי במהלך החישוב, שבסופו מתקבלים שלושה פתרונות ממשיים.

הרבה התקשו לקבל את השיטה, וטענו כי אינה ריגורוזית משום שמספרים כגון אינם קיימים!

זה ביסודו, אופן הולדתם של המספרים המרוכבים.