חומר עזר 3.1 : הקדמה למספרים מרוכבים – משוואות ריבועיות

תהי משוואה ריבועית כללית:

(כאשר המקדמים a,b,c הינם מספרים ממשיים ו )

על ידי השלמה לריבוע נקבל: או

וכן נוכל להסיק:

לביטוי שנסמן ב נקרא הדיסקרימיננטה של המשוואה הריבועית, וסימנה מעיד על סוג

הפתרון:

1.: יש למשוואה שני פתרונות ממשיים שונים (הניתנים ע"י (#) )

2.: יש למשוואה פתרון ממשי יחיד:

3. : לא קיים פתרון ממשי למשוואה

ניתן להבין את שלושת המצבים הללו בצורה אינטואיטיבית יותר על ידי התבוננות בגרף של הפונקציה:

שהיא פרבולה:

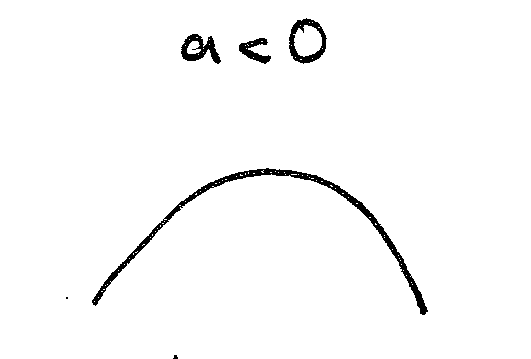
הפתרונות ל-(*) נתונים על ידי נקודת/נקודות החיתוך של הגרף עם ציר ה–x.

עבור המצב יש 3 אפשרויות:

והן מתאימות לתכונות הנוסחה (#) שקיבלנו מעל.

יש לשים לב שפירוק המשוואה לגורמים שקול למציאת פתרונות ממשיים:

פירוק של משוואה ריבועית חייב להיות מהצורה של מכפלת שני גורמים ליניאריים, ולכל פולינום p

מתקיים: .

שני שורשים:

שורש יחיד:

אין שורשים ממשיים: המשוואה אי–פריקה מעל הממשיים.