נרצה להשתמש בידע שרכשנו זה עתה ביחידה 2.4, (אודות היפרבולה מהצורה

) יחד עם טרנספורמציה פשוטה (הפעם, יהא זה סיבוב) על מנת להבין את המקום הגיאומטרי המוגדר על ידי המשוואה

נביט בשני הישרים

, אשר ניצבים זה לזה וחותכים את צירי

ו-

בהנתן נקודה כלשהי במישור, נוכל לתארה באמצעות הקואורדינטות

, בהתאם לצירי

. כך נוכל לעשות גם אם נחשוב על הישרים החדשים כעל צירים: לנקודה הנתונה ישנן קואורדינטות אף ביחס לישרים אלו, ונסמנן

כך שהישר

הנו "ציר ה-

", והישר

הוא "ציר ה-

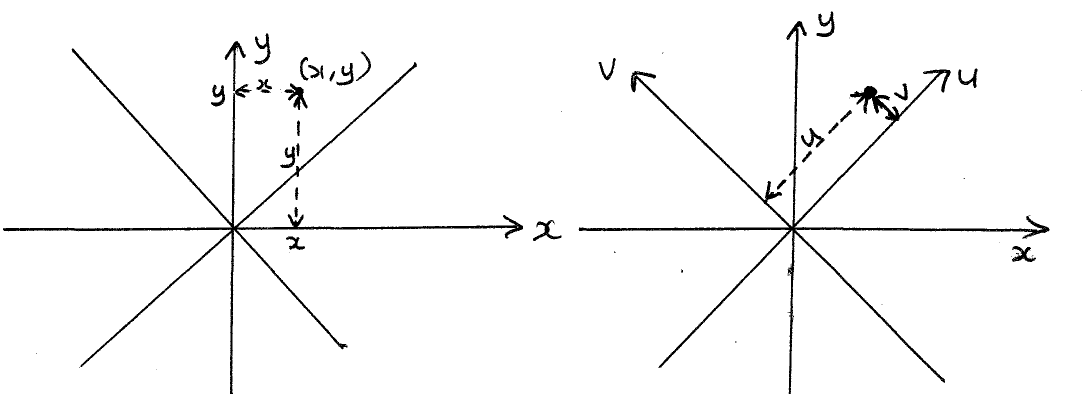
נשאלת השאלה: מהו הקשר בין הקואורדינטות

? על מנת לענות על שאלה זו, נמצא ביטוי מפורש ל-

בעזרת

. ישנן דרכים רבות לעשות זאת, ע"י שימוש בווקטורים, טריגונומטריה, וכו'. אנו נבחר דרך הנעזרת ביחידה 1.13 (הטלות):

נשים לב כי

איננו אלא אורך ההטלה של ווקטור המיקום

בכיוון ציר ה-

, קרי:

מאידך,

הנו אורך הטלת ווקטור המיקום

בכיוון ציר

ולכן

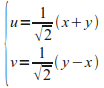נשים לב כי את המשוואה

, בה אנו מתעניינים, ניתן לבטא גם ע"י:

כלומר, ביחס לקואורדינטות

, נקבל את ההיפרבולה

(אותה חקרנו ביחידה הקודמת):

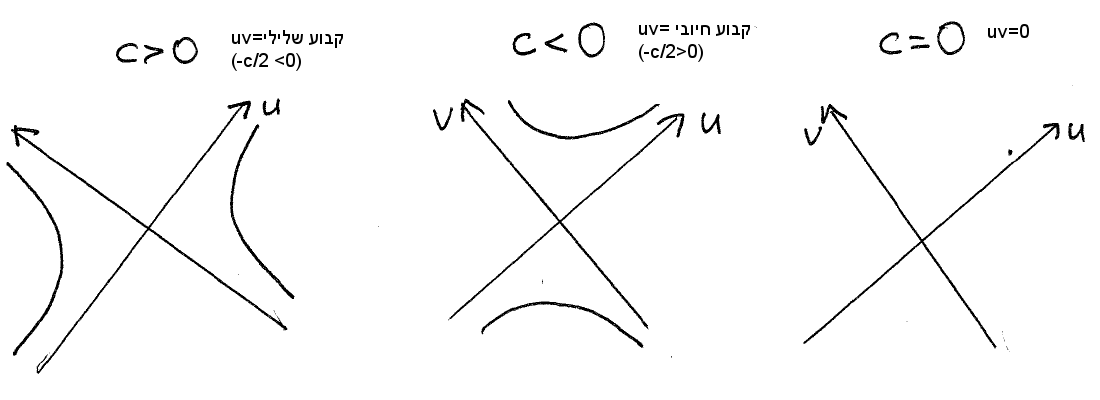
(נשים לב כי הסימן של

הפוך לסימן של הצורה הקנונית של הפרבולה)

ולבסוף, על מנת להשלים את התמונה, נצייר אף את הצירים במקומם:


שני ישרים	היפרבולה	היפרבולה

ישנן דרכים רבות בהן ניתן להגדיר היפרבולה (ניתן להגדירה כמקום גיאומטרי של נקודות המקיימות תנאי מסוים בנוגע לקביעות יחס המרחקים בין נקודה קבועה (המכונה מוקד) וישר קבוע (הקרוי דירקטריקס, directrix); או כאוסף הנקודות שהפרש מרחקיהן משתי נקודות קבועות (מוקדים) הוא קבוע , וכו'). עבורנו, היפרבולה תהא צורה אשר ניתן לקבלה מה"היפרבולה הסטנדרטית"