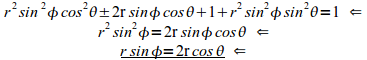א)

הנקודה .

נמצא את הקואורדינטות הכדוריות של הנקודה:

הרדיוס הנו.

הנה הקואורדינטה הזוויתית הקוטבית

של הנקודה , כלומר

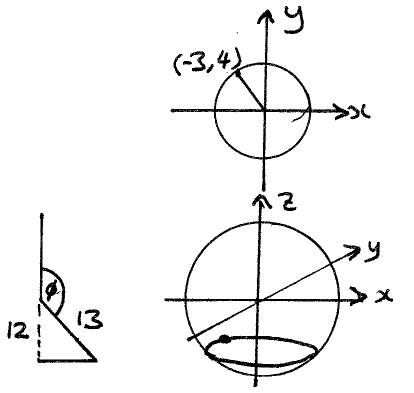
(ב)

הנקודה . הקואורדינטות הקרטזיות של הנקודה תמצאנה בזו הדרך:

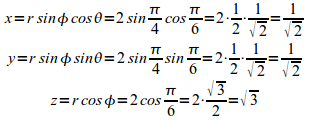
(נזכור כי )

(ג)

כאשר , קבוע, המקום הגיאומטרי הנו ספירה ברדיוס .

(ד)

אם קבועה, משמעות הדבר הנה כי הקואורדינטה הזוויתית הקוטבית של הנה (וכמובן שאין תנאי על ). מכאן כי המקום הגיאומטרי הוא חצי מישור המכיל את ציר .

(ה)

לבסוף, אם נכפה כי תהא קבועה, אזי נקבל כי הרדיוס-ווקטור יוצר זווית קבועה עם , ולכן המקום הגיאומטרי שנקבל הוא חרוט עם חצי-זווית מפתח שצירו הוא ציר ה- .

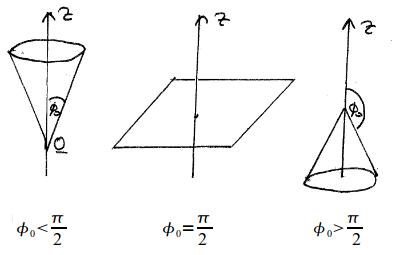
כלומר תתקבלנה הצורות הבאות

אם: החלק החיובי של ציר .

אם: החלק השלילי של ציר .

(ו)

את הגליל שתואר ביחידה 2.12, סעיף (ט) - נוכל לרשום בקואורדינטות כדוריות בעזרת הנוסחאות מיחידה 2.14: