במרחב התלת-ממדי,
בהשתמשנו
בקואורדינטות "זוויתיות",
אך
הפעם נביט תחילה בנקודה על הספירה (שמרכזה
בראשית), ורדיוסה:
ולאחר
מכן נבחן כיצד להגדיר קואורדינטות "טבעיות"
אשר
תתארנה את מיקומה של הנקודה על הספירה.חומר עזר 2.13 : הגדרת קואורדינטות כדוריות (ספריות)
כביחידה
2.10, נרצה
לתת קואורדינטות לנקודה
במרחב התלת-ממדי,
בהשתמשנו
בקואורדינטות "זוויתיות",
אך
הפעם נביט תחילה בנקודה על הספירה (שמרכזה
בראשית), ורדיוסה:
ולאחר
מכן נבחן כיצד להגדיר קואורדינטות "טבעיות"
אשר
תתארנה את מיקומה של הנקודה על הספירה.
דרך
זו שונה מזו שעשינו ביחידה 2.10,
בה
ראינו את הנקודהשוכנת
בגליל שצירו הוא ציר ה
ולכן
בעל רדיוס
;
|
או-אז,
בגליל
זה, הקואורדינטות
את
הנקודה
ו-
אם-כך,
ו-
נקודה
כללית במרחב (
ו
אלו היו קואורדינטות גליליות. |
|
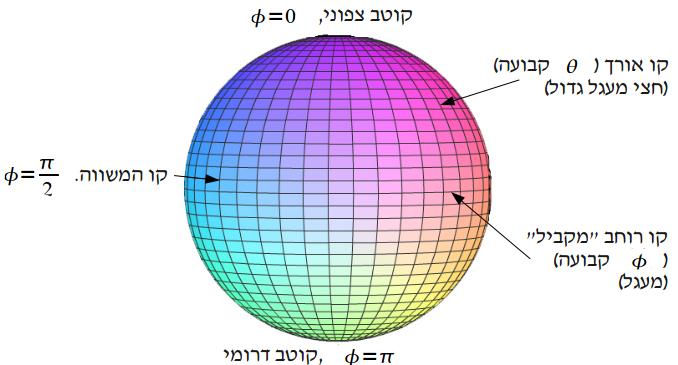
בבואנו להגדיר קואורדינטות ספריות, אנו חושבים על המרחב כולו כאיחוד של ספירות ברדיוסים שונים, שמרכזיהן בראשית הצירים.
על
מנת לתאר נקודה במרחב, ראשית
עלינו להבחין על איזו ספירה היא יושבת,
קרי
הרדיוס, שאיננו
אלא
.
לאחר-מכן,
על
ספירה זו ישנן קואורדינטות טבעיות:
-
קוי
גובה,
-
קוי
רוחב.
כפי
שאנו מכירים מכדור הארץ.
עם-זאת,
המוסכמה
המתמטית למדידת
שונה
במקצת מזו המשמשת בדרך כלל למדידת קווי
אורך וגובה:
|
|
(א) |
לעולם נשתמש ברדיאנים. |
|
|
|
(ב) |
קו
הרוחב נמדד כזווית בין הרדיוס וציר
ה-
ההבדל כאן
הנו שקו רוחב 0 הנו
קו המשווה, בעוד
שאז
|
|
|
|
(ג) |
גובה
|
|
|
|
|
אנו
רואים כי למעשה
וציר
אם נחשוב על חצי המישור המכיל את החלק החיובי של
ציר
ה- וניתן
לחצי-מישור
זה להסתובב סביב ציר ה- אזי
מכיוונו
החיובי של ציר
יכיל
את הנקודה |
|
לסיכום,
הן
קואורדינטות כדוריות (ספריות)
של
נקודה
כאשר:
|
|
- הנו אורך הרדיוס = מרחק הנקודה מהראשית |
|
|
- היא
קואורדינטה קוטבית זוויתית של
|
|
|
- היא
הזווית בין הרדיוס-ווקטור
(ווקטור
המיקום) לבין
|
|
הטווחים המותרים הם: |
|
|
|
|
|
|
|
וכן
ישנן נקודות סינגולריות על ציר
(
).
בהגדרה
שהבאנו כאן,
הנה
אותה הזווית כבקואורדינטות הגליליות,
שהוגדרו
ביחידה 2.10.
מספיקות
על מנת לקבע 
ו
במישור
;
