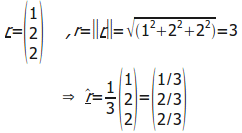חומר עזר 1.8 : פעולות על וקטורים – כפל בסקלר
כמו
בסכומים של וקטורים,
נגדיר
את הכפולה הסקלרית של וקטור על-ידי
סקלר
![]() ברכיבים:
ברכיבים:
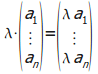
דוגמא:
![]() תמיד
תמיד
ואילו
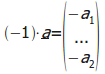 מסומן
מסומן
![]() (מינוס
הווקטור).
(מינוס
הווקטור).
משמעות
גאומטרית:
![]() הוא
וקטור אשר כיוונו זהה לזה של
הוא
וקטור אשר כיוונו זהה לזה של
![]() עבור
עבור
![]() וכיוונו הפוך
וכיוונו הפוך
ל-![]() עבור
עבור
![]() .
האורך
של
.
האורך
של
![]() הוא,
לפי
הגדרותינו:
הוא,
לפי
הגדרותינו:
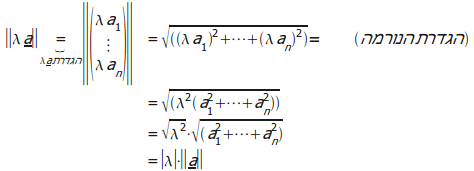 .
.
וקטור
יחידה מקביל לווקטור נתון:
נניח
ש-![]() הוא
וקטור (שאינו
וקטור האפס).
אנו
רוצים למצוא את וקטור היחידה בכיוון של
הוא
וקטור (שאינו
וקטור האפס).
אנו
רוצים למצוא את וקטור היחידה בכיוון של
![]() .
ניתן
לכתוב כל וקטור המקביל ל-
.
ניתן
לכתוב כל וקטור המקביל ל-![]() כ-
כ-![]() עבור
סקלר כלשהו,
עבור
סקלר כלשהו,
![]() .
מתי
יהיה וקטור זה וקטור היחידה?
.
מתי
יהיה וקטור זה וקטור היחידה?
|
כאשר |
|
לכן
יש שני וקטורי יחידה מקבילים ל-![]() ,
זאת
אומרת
,
זאת
אומרת
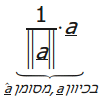 ו-
ו-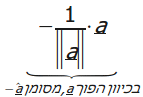 .
.
|
|
אותה
האות
|
שימו
לב:
בשיבוש
הסימן,
לעתים
קרובות נכתוב
![]() ,
למרות
שהמשמעות של חילוק וקטור בסקלר
,
למרות
שהמשמעות של חילוק וקטור בסקלר
![]() היא כפל בהופכי של אותו סקלר,
היא כפל בהופכי של אותו סקלר,
![]() וככפל
בסקלר, הוא
מבוצע על-ידי
חילוק רכיב-רכיב
ב-
וככפל
בסקלר, הוא
מבוצע על-ידי
חילוק רכיב-רכיב
ב-![]() .
.

בדרך
כלל:
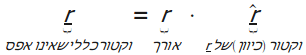
דוגמה: