חומר
עזר 1.6
: סימון
כללי של וקטורים וסימונים מיוחדים ב-![]()
בסעיפים קודמים ראינו שני סימונים עבור וקטורים:
![]() (בו
חץ מצוין על-ידי
נקודות הקצה שלו,
סימון
בו ייתור רב,
כיוון
שווקטור אינו מספק לנו מידע על מיקומו
במרחב,
אלא
רק על כיוונו וגודלו).
(בו
חץ מצוין על-ידי
נקודות הקצה שלו,
סימון
בו ייתור רב,
כיוון
שווקטור אינו מספק לנו מידע על מיקומו
במרחב,
אלא
רק על כיוונו וגודלו).
![]() הסימון
המסויים של וקטור המיקום
הסימון
המסויים של וקטור המיקום
![]() של הנקודה
של הנקודה
![]() (וראינו
כבר כי ניתן לכתוב את כל הווקטורים
הגאומטריים ב-
(וראינו
כבר כי ניתן לכתוב את כל הווקטורים
הגאומטריים ב-![]() -ממדים
בצורה זו).
-ממדים
בצורה זו).
לעתים
אנו לא רוצים לכתוב את הרכיבים באופן
מפורש,
וגם
לא לתת את נקודות הקצה של החץ המסמל את
הווקטור.
אז
נוכל להשתמש באות יחידה – בדרך כלל אות
קטנה מודגשת (אם
מודפסת)
או
מסומנת בקו תחתון:
![]() ,
למרות
שישנם אנשים המשתמשים בקו עליון או אפילו
בחץ עליון על-מנת
להזכיר לעצמם כי לווקטור יש כיוון:
,
למרות
שישנם אנשים המשתמשים בקו עליון או אפילו
בחץ עליון על-מנת
להזכיר לעצמם כי לווקטור יש כיוון:
![]() או
או
![]() .
[שימו
לב:
.
[שימו
לב:
![]() עשוי
להיות מבלבל עבורנו,
כיוון
שבפרק 3
נשתמש
בסימון זה עבור צימוד מרוכב,
וישנם
מקרים בהם נדון בווקטורים ובמספרים
מרוכבים בעת ובעונה אחת – וקטורים עם
רכיבים שהם מספרים מרוכבים
מופיעים במכניקת הקוונטים,
אלקטרו-מגנטיות
ואופטיקה].
עשוי
להיות מבלבל עבורנו,
כיוון
שבפרק 3
נשתמש
בסימון זה עבור צימוד מרוכב,
וישנם
מקרים בהם נדון בווקטורים ובמספרים
מרוכבים בעת ובעונה אחת – וקטורים עם
רכיבים שהם מספרים מרוכבים
מופיעים במכניקת הקוונטים,
אלקטרו-מגנטיות
ואופטיקה].
ניזכר
כי![]() משמעו וקטור האפס,
משמעו וקטור האפס,
![]() (חץ
(חץ
![]() שאורכו אפס ולכן,
טכנית,
הינו
ללא כיוון).
שאורכו אפס ולכן,
טכנית,
הינו
ללא כיוון).
המספרים
![]() נקראים רכיבי
נקראים רכיבי
![]() ,
כאשר
בדרך כלל נשתמש באותה אות יחד עם מציין
(אינדקס)
כלשהו:
,
כאשר
בדרך כלל נשתמש באותה אות יחד עם מציין
(אינדקס)
כלשהו:
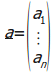 ,
,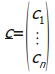 .
.
בדרך
כלל
![]() יהיה וקטור המיקום של הנקודה
יהיה וקטור המיקום של הנקודה
![]() (תצורתה
הגדולה של האות).
(תצורתה
הגדולה של האות).
כרגיל,
היוצא
מן הכלל מעיד על הכלל ונשתמש ב-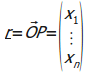 כווקטור
גנרי:
כווקטור
גנרי:
|
|
|
כיוון שאלו הם הסימולים המקובלים.
גודל
הווקטור
![]() מסומן כ-
מסומן כ-![]() ,
ונקרא
לעתים הנורמה
או האורך
של
,
ונקרא
לעתים הנורמה
או האורך
של
![]() .
זהו
מספר ממשי אי-שלילי
הניתן כביטוי של רכיבי הווקטור:
.
זהו
מספר ממשי אי-שלילי
הניתן כביטוי של רכיבי הווקטור:
הגדרה:
![]()
[מכיוון שזוהי הנוסחה עבור OA מסעיף 1.3]
![]() בדיוק
כאשר
בדיוק
כאשר
![]() .
.
וקטור
יקרא וקטור יחידה
כאשר אורכו הוא 1
ועל-מנת
להזכיר לנו כי וקטור מסוים הינו וקטור
יחידה,
נסמן
מעליו כובע:
![]() וכיוון
שהוא לא מכיל מידע מעניין על האורך,
הוא
מכיל רק מידע על הכיוון.
לכן
כיוון יצוין באופן הכי מדויק על-ידי
וקטור כיוון
וכיוון
שהוא לא מכיל מידע מעניין על האורך,
הוא
מכיל רק מידע על הכיוון.
לכן
כיוון יצוין באופן הכי מדויק על-ידי
וקטור כיוון
![]() ,
וקטור
יחידה בכיוון הרצוי.
כמובן,
כל
וקטור שאינו וקטור האפס מציין כיוון –
פשוט התעלם מאורכו.
,
וקטור
יחידה בכיוון הרצוי.
כמובן,
כל
וקטור שאינו וקטור האפס מציין כיוון –
פשוט התעלם מאורכו.
ישנו סימון מיוחד בו משתמשים עבור וקטורי כיוון בכיוון צירי הקואורדינטות החיוביים:
![]() הינו
וקטור היחידה בכיוון של ציר
הינו
וקטור היחידה בכיוון של ציר
![]() החיובי,
כך
ש-
החיובי,
כך
ש- - כל
הרכיבים הינם 0
מלבד
הרכיב ה-
- כל
הרכיבים הינם 0
מלבד
הרכיב ה-![]() שהינו
1.
שהינו
1.
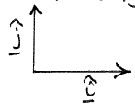
סימון
ב-![]() :
בדרך
כלל הקואורדינטות יסומנו
:
בדרך
כלל הקואורדינטות יסומנו
![]() (במקום
(במקום
![]() )
ווקטורי
היחידה בכיווני צירי הקואורדינטות
החיוביים יסומנו
)
ווקטורי
היחידה בכיווני צירי הקואורדינטות
החיוביים יסומנו
![]() :
:
![]() ,
ונקודה
גנרית
,
ונקודה
גנרית
![]() תהיה בעלת וקטור מיקום
תהיה בעלת וקטור מיקום
![]() .
.
סימון
ב-![]() :
בדרך
כלל הקואורדינטות ב-
:
בדרך
כלל הקואורדינטות ב-![]() יסומנו
ב-
יסומנו
ב-![]() (במקום
(במקום
![]() )
ו-
)
ו-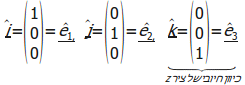 ,
ונקודה
גנרית
,
ונקודה
גנרית
![]() תהיה בעלת וקטור מיקום
תהיה בעלת וקטור מיקום
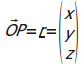 .
.
שימו
לב:
אין
משמעות בכתיבת
![]() אם לא ברור באיזה ממד אנו
עובדים.
אם לא ברור באיזה ממד אנו
עובדים.
דוגמאות של וקטורים המציינים גדלים פיזיקליים שכיחים וסימוניהם:
![]() וקטור
מיקום של נקודה (גודל
=
רדיוס)
וקטור
מיקום של נקודה (גודל
=
רדיוס)
![]() וקטור
מהירות (גודל
=
גודל
המהירות [speed])
וקטור
מהירות (גודל
=
גודל
המהירות [speed])
![]() וקטור
מהירות זוויתית (רגעית)
(גודל
=
מהירות
זוויתית
וקטור
מהירות זוויתית (רגעית)
(גודל
=
מהירות
זוויתית
![]() ;
כיוון
||
ציר
הסיבוב)
;
כיוון
||
ציר
הסיבוב)
![]() וקטור
העתק
וקטור
העתק
![]() כוח
כוח
![]() תנע
קווי
תנע
קווי
![]() תנע
זוויתי
תנע
זוויתי
בדרך
כלל אורכו של
![]() מסומן
מסומן
![]() (אך
שימוש זה אינו אוניברסלי).
(אך
שימוש זה אינו אוניברסלי).