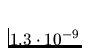 for the first experiment
and
for the first experiment
and 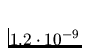 for the second
(which gives the probability
for the second
(which gives the probability 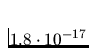 for the
union of the samples)."
for the
union of the samples)."
Witztum, Rips and Rosenberg claim to have found an arrow sent by the author of the Book of Genesis, crossing thousands of years in its flight. But this arrow was not sent by the author of the Book of Genesis. The arrow was stuck by Witztum, Rips and Rosenberg themselves and they left their fingerprints.
In their 1987 preprint [3] which presented the situation after the second test was carried out, Witztum, Rips and Rosenberg write in the introduction as follows:
"For the string G however, for the unperturbed sample
we obtained c(w,w') tending to zero with a probability against a null
hypothesis of a uniform distribution that we estimate as
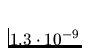 for the first experiment
and
for the first experiment
and 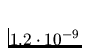 for the second
(which gives the probability
for the second
(which gives the probability 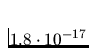 for the
union of the samples)."
for the
union of the samples)."
These numbers refer to the principal measure of significance
used by WRR at that time for the two tests they made.
The measure of significance used was later called the P2-statistics
or the P2-score.
In the Analysis Section of the same preprint
the next digit is revealed so the numbers
are  and
and  , respectively.
, respectively.
The ratio between these two numbers is 1.1217. We will see that in view of the instability of the P2-statistics this ratio is extremely small. It is significantly small compared to random partitions of the 66 Rabbis into sets of 34 and 32 Rabbis respectively, it is significantly small compared to random perturbations of the original division of Rabbis, it is even substantially smaller than the typical effect of adding and deleting a single appellation to a single Rabbi.
The only explanation we can offer for this phenomenon is that there was an optimization process in the second experiment which stopped when the significance level of the first experiment was reached. Moreover, consider an optimization process in the second test which terminates with the addition of an appellation which brings the significance level beyond that of the first test. We can expect that the ratio of the significance levels of the two tests will be in the neighborhood of the square root of the effect of the last appellation. Indeed, the square root of the typical effect of adding an appellation is comparable to the ratio we witness.
It is worth noting that the astronomical significance levels cited above
(from the 87 preprint [3]) are false due to wrong independence assumptions.
A realistic way to measure the significance level suggested by Diaconis
gives (for the second experiment) the value 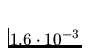 .(See Section 7.)
.(See Section 7.)